Senin, 19 Desember 2016
Rabu, 11 Mei 2016
TERMODINAMIKA : soal dan pembahasan
Setelah sebelumnya saya memposting materi mengenai TERMODINAMIKA , maka kali ini saya akan memberikan kembali sekilas rumus umum, contoh soal dan pembahasan mengenai termodinamika agar lebih mempermudah kalian untuk memahami materi termodinamika. semoga bermanfaat...
Rumus - Rumus Minimal
Hukum Termodinamika I
ΔU = Q − W
Keterangan :
ΔU = perubahan energi dalam (joule)
Q = kalor (joule)
W = usaha (joule)
Proses-proses
Isobaris → tekanan tetap
Isotermis → suhu tetap → ΔU = 0
Isokhoris → volume tetap (atau isovolumis atau isometric) → W = 0
Adiabatis → tidak terjadi pertukaran kalor → Q = 0
Siklus → daur → ΔU = 0
Persamaan Keadaan Gas
Hukum Gay-Lussac
Tekanan tetap → V/T = Konstan → V1/T1 = V2/T2
Hukum Charles
Volume tetap → P/T = Konstan → P1/T1 = P2/T2
Hukum Boyle
Suhu tetap → PV = Konstan → P1V1 = P2V2
P, V, T Berubah (non adiabatis)
(P1V1) / (T1) = (P2V2) / (T2)
Adiabatis
P1V1 γ= P2V2γ
T1V1 γ − 1= T2V2γ − 1
γ = perbandingan kalor jenis gas pada tekanan tetap dan volum tetap → γ = Cp/Cv
Usaha
W = P(ΔV) → Isobaris
W = 0 → Isokhoris
W = nRT ln (V2 / V1) → Isotermis
W = − 3/2 nRΔT → Adiabatis ( gas monoatomik)
Keterangan :
T = suhu (Kelvin, jangan Celcius)
P = tekanan (Pa = N/m2)
V = volume (m3)
n = jumlah mol
1 liter = 10−3m3
1 atm = 105 Pa ( atau ikut soal!)
Jika tidak diketahui di soal ambil nilai ln 2 = 0,693
Mesin Carnot
η = ( 1 − Tr / Tt ) x 100 %
η = ( W / Q1 ) x 100%
W = Q1 − Q2
Keterangan :
η = efisiensi mesin Carnot (%)
Tr = suhu reservoir rendah (Kelvin)
Tt = suhu reservoir tinggi (Kelvin)
W = usaha (joule)
Q1 = kalor masuk / diserap reservoir tinggi (joule)
Q2 = kalor keluar / dibuang reservoir rendah (joule)
Soal No. 1
Suatu gas memiliki volume awal 2,0 m3 dipanaskan dengan kondisi isobaris hingga volume akhirnya menjadi 4,5 m3. Jika tekanan gas adalah 2 atm, tentukan usaha luar gas tersebut!
(1 atm = 1,01 x 105 Pa)
Pembahasan
Data :
V2 = 4,5 m3
V1 = 2,0 m3
P = 2 atm = 2,02 x 105 Pa
Isobaris → Tekanan Tetap
W = P (ΔV)
W = P(V2 − V1)
W = 2,02 x 105 (4,5 − 2,0) = 5,05 x 105 joule
Soal No. 2
1,5 m3 gas helium yang bersuhu 27oC dipanaskan secara isobarik sampai 87oC. Jika tekanan gas helium 2 x 105 N/m2 , gas helium melakukan usaha luar sebesar....
A. 60 kJ
B. 120 kJ
C. 280 kJ
D. 480 kJ
E. 660 kJ
(Sumber Soal : UMPTN 1995)
Pembahasan
Data :
V1 = 1,5 m3
T1 = 27oC = 300 K
T2 = 87oC = 360 K
P = 2 x 105 N/m2
W = PΔV
Mencari V2 :
V2/T2 = V1/T1
V2 = ( V1/T1 ) x T2 = ( 1,5/300 ) x 360 = 1,8 m3
W = PΔV = 2 x 105(1,8 − 1,5) = 0,6 x 105 = 60 x 103 = 60 kJ
Soal No. 3
2000/693 mol gas helium pada suhu tetap 27oC mengalami perubahan volume dari 2,5 liter menjadi 5 liter. Jika R = 8,314 J/mol K dan ln 2 = 0,693 tentukan usaha yang dilakukan gas helium!
Pembahasan
Data :
n = 2000/693 mol
V2 = 5 L
V1 = 2,5 L
T = 27oC = 300 K
Usaha yang dilakukan gas :
W = nRT ln (V2 / V1)
W = (2000/693 mol) ( 8,314 J/mol K)(300 K) ln ( 5 L / 2,5 L )
W = (2000/693) (8,314) (300) (0,693) = 4988,4 joule
Soal No. 4
Mesin Carnot bekerja pada suhu tinggi 600 K, untuk menghasilkan kerja mekanik. Jika mesin menyerap kalor 600 J dengan suhu rendah 400 K, maka usaha yang dihasilkan adalah....
A. 120 J
B. 124 J
C. 135 J
D. 148 J
E. 200 J
(Sumber Soal : UN Fisika 2009 P04 No. 18)
Pembahasan
η = ( 1 − Tr / Tt ) x 100 %
Hilangkan saja 100% untuk memudahkan perhitungan :
η = ( 1 − 400/600) = 1/3
η = ( W / Q1 )
1/3 = W/600
W = 200 J
Soal No. 5
Diagram P−V dari gas helium yang mengalami proses termodinamika ditunjukkan seperti gambar berikut!

Usaha yang dilakukan gas helium pada proses ABC sebesar....
A. 660 kJ
B. 400 kJ
C. 280 kJ
D. 120 kJ
E. 60 kJ
(Sumber Soal : UN Fisika 2010 P04 No. 17)
Pembahasan
WAC = WAB + WBC
WAC = 0 + (2 x 105)(3,5 − 1,5) = 4 x 105 = 400 kJ
Soal No. 6
Suatu mesin Carnot, jika reservoir panasnya bersuhu 400 K akan mempunyai efisiensi 40%. Jika reservoir panasnya bersuhu 640 K, efisiensinya.....%
A. 50,0
B. 52,5
C. 57,0
D. 62,5
E. 64,0
(Sumber Soal : SPMB 2004)
Pembahasan
Data pertama:
η = 40% = 4 / 10
Tt = 400 K
Cari terlebih dahulu suhu rendahnya (Tr) hilangkan 100 % untuk mempermudah perhitungan:
η = 1 − (Tr/Tt)
4 / 10 = 1 − (Tr/400)
(Tr/400) = 6 / 10
Tr = 240 K
Data kedua :
Tt = 640 K
Tr = 240 K (dari hasil perhitungan pertama)
η = ( 1 − Tr/Tt) x 100%
η = ( 1 − 240/640) x 100%
η = ( 5 / 8 ) x 100% = 62,5%
Soal No. 7
Sebuah mesin Carnot yang menggunakan reservoir suhu tinggi bersuhu 800 K mempunyai efisiensi sebesar 40%. Agar efisiensinya naik menjadi 50%, maka suhu reservoir suhu tinggi dinaikkan menjadi....(UMPTN 90)
A. 900 K
B. 960 K
C. 1000 K
D. 1180 K
E. 1600 K
Pembahasan
Rumus efisiensi (tanpa %)

Data dari Efisiensi pertama,
Tt = 800 K
η = 40% = 0,4 → (1 − η) = 0,6
Dari sini diperoleh suhu rendah Tr

Dari data efisiensi kedua,
η = 50% = 0,5 → (1 − η) = 0,5
Tr = 480 K
Suhu tingginya:

Soal No. 8
Sebuah mesin Carnot bekerja pada pada suhu tinggi 627°C memiliki efisiensi 50%. Agar efisiensi maksimumnya naik menjadi 70% pada suhu rendah yang tetap, maka suhu tingginya harus dinaikkan menjadi....
A. 1500°C
B. 1227°C
C. 1127°C
D. 1073°C
E. 927°C
Soal No. 9
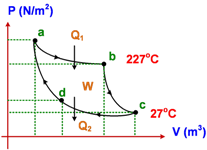
Perhatikan gambar berikut ini!

Jika kalor yang diserap reservoir suhu tinggi adalah 1200 joule, tentukan :
a) Efisiensi mesin Carnot
b) Usaha mesin Carnot
c) Perbandingan kalor yang dibuang di suhu rendah dengan usaha yang dilakukan mesin Carnot
d) Jenis proses ab, bc, cd dan da
Pembahasan
a) Efisiensi mesin Carnot
Data :
Tt = 227oC = 500 K
Tr = 27oC = 300 K
η = ( 1 − Tr/Tt) x 100%
η = ( 1 − 300/500) x 100% = 40%
b) Usaha mesin Carnot
η = W/Q1
4/10 = W/1200
W = 480 joule
c) Perbandingan kalor yang dibuang di suhu rendah dengan usaha yang dilakukan mesin Carnot
Q2 = Q1 − W = 1200 − 480 = 720 joule
Q2 : W = 720 : 480 = 9 : 6 = 3 : 2
d) Jenis proses ab, bc, cd dan da
ab → pemuaian isotermis (volume gas bertambah, suhu gas tetap)
bc → pemuaian adiabatis (volume gas bertambah, suhu gas turun)
cd → pemampatan isotermal (volume gas berkurang, suhu gas tetap)
da → pemampatan adiabatis (volume gas berkurang, suhu gas naik)
Soal No. 10
Sejumlah gas ideal mengalami proses seperti gambar berikut.

Proses yang menggambarkan adiabatis dan isokhorik berturut-turut ditunjukkan pada nomor...(UN Fisika 2013)
A. 1 – 2 dan 3 – 4
B. 1 – 2 dan 4 – 5
C. 2 – 3 dan 1 – 2
D. 2 – 3 dan 1 – 2
E. 2 – 3 dan 3 – 4
Pembahasan
Adiabatis : proses dimana tidak ada kalor masuk atau keluar. Ciri garisnya melengkung curam. Seperti garis 2 - 3.
Isokhorik : proses pada volume tetap. Garisnya yang tegak lurus sumbu V. Bisa 5 - 1, juga 3 - 4.
Pilihan yang ada sesuai adiabatis dan isokhoris adalah 2 - 3 dan 3 - 4.
Soal No. 11

Suatu gas ideal mengalami proses siklus seperti pada gambar P − V di atas. Kerja yang dihasilkan pada proses siklus ini adalah....kilojoule.
A. 200
B. 400
C. 600
D. 800
E. 1000
Pembahasan
W = Usaha (kerja) = Luas kurva siklus = Luas bidang abcda
W = ab x bc
W = 2 x (2 x 105) = 400 kilojoule
Soal No. 12
Suatu pesawat pendingin Carnot mempunyai koefisien kinerja 6,5. Jika reservoir yang tinggi 27°C, maka reservoir yang bersuhu rendah adalah....
A. −5 °C
B. −8 °C
C. −10 °C
D. −12 °C
E. −13 °C
(Dari soal Soal UMPTN 1994)
Pembahasan
Data dari soal adalah:
Tt = 27°C = 27 + 273 = 300 K
Cp = 6,5
Tr = .....
Dari rumus koefisien performansi mesin atau pesawat pendingin:

Dimana
Cp = koefisien performansi
Tt = suhu tinggi (Kelvin)
Tr = suhu rendah (Kelvin)
Masuk datanya:

Soal No. 13
Sebuah mesin pendingin memiliki reservoir suhu rendah sebesar −15°C. Jika selisih suhu antara reservoir suhu tinggi dan suhu rendahnya sebesar 40°C, tentukan koefisien performansi mesin tersebut!
Pembahasan
Data mesin
Tr = − 15°C = (− 15 + 273) K = 258 K
Tt − Tr = 40°C
Cp =....

Soal No. 14
Sebuah kulkas memiliki suhu rendah − 13°C dan suhu tinggi 27°C. Jika kalor yang dipindahkan dari reservoir suhu rendah adalah 1300 joule, tentukan usaha yang diperlukan kulkas!
Pembahasan
Data mesin pendingin
Tr = − 13°C = (− 13 + 273) K = 260 K
Tt = 27°C = 300 K
Qr = 1300 j
W = ....
Rumus koefisien performansi jika diketahui usaha dan kalor

Dimana
W = usaha yang diperlukan untuk memindahkan kalor dari suhu rendah
Qr = kalor yang dipindahkan dari suhu rendah
Sehingga jika digabung dengan rumus dari no sebelumnya diperoleh:

sumber : http://fisikastudycenter.com/fisika-xi-sma/33-termodinamika
Rumus - Rumus Minimal
Hukum Termodinamika I
ΔU = Q − W
Keterangan :
ΔU = perubahan energi dalam (joule)
Q = kalor (joule)
W = usaha (joule)
Proses-proses
Isobaris → tekanan tetap
Isotermis → suhu tetap → ΔU = 0
Isokhoris → volume tetap (atau isovolumis atau isometric) → W = 0
Adiabatis → tidak terjadi pertukaran kalor → Q = 0
Siklus → daur → ΔU = 0
Persamaan Keadaan Gas
Hukum Gay-Lussac
Tekanan tetap → V/T = Konstan → V1/T1 = V2/T2
Hukum Charles
Volume tetap → P/T = Konstan → P1/T1 = P2/T2
Hukum Boyle
Suhu tetap → PV = Konstan → P1V1 = P2V2
P, V, T Berubah (non adiabatis)
(P1V1) / (T1) = (P2V2) / (T2)
Adiabatis
P1V1 γ= P2V2γ
T1V1 γ − 1= T2V2γ − 1
γ = perbandingan kalor jenis gas pada tekanan tetap dan volum tetap → γ = Cp/Cv
Usaha
W = P(ΔV) → Isobaris
W = 0 → Isokhoris
W = nRT ln (V2 / V1) → Isotermis
W = − 3/2 nRΔT → Adiabatis ( gas monoatomik)
Keterangan :
T = suhu (Kelvin, jangan Celcius)
P = tekanan (Pa = N/m2)
V = volume (m3)
n = jumlah mol
1 liter = 10−3m3
1 atm = 105 Pa ( atau ikut soal!)
Jika tidak diketahui di soal ambil nilai ln 2 = 0,693

Mesin Carnot
η = ( 1 − Tr / Tt ) x 100 %
η = ( W / Q1 ) x 100%
W = Q1 − Q2
Keterangan :
η = efisiensi mesin Carnot (%)
Tr = suhu reservoir rendah (Kelvin)
Tt = suhu reservoir tinggi (Kelvin)
W = usaha (joule)
Q1 = kalor masuk / diserap reservoir tinggi (joule)
Q2 = kalor keluar / dibuang reservoir rendah (joule)
Contoh soal dan pembahasan
Soal No. 1
Suatu gas memiliki volume awal 2,0 m3 dipanaskan dengan kondisi isobaris hingga volume akhirnya menjadi 4,5 m3. Jika tekanan gas adalah 2 atm, tentukan usaha luar gas tersebut!
(1 atm = 1,01 x 105 Pa)
Pembahasan
Data :
V2 = 4,5 m3
V1 = 2,0 m3
P = 2 atm = 2,02 x 105 Pa
Isobaris → Tekanan Tetap
W = P (ΔV)
W = P(V2 − V1)
W = 2,02 x 105 (4,5 − 2,0) = 5,05 x 105 joule
Soal No. 2
1,5 m3 gas helium yang bersuhu 27oC dipanaskan secara isobarik sampai 87oC. Jika tekanan gas helium 2 x 105 N/m2 , gas helium melakukan usaha luar sebesar....
A. 60 kJ
B. 120 kJ
C. 280 kJ
D. 480 kJ
E. 660 kJ
(Sumber Soal : UMPTN 1995)
Pembahasan
Data :
V1 = 1,5 m3
T1 = 27oC = 300 K
T2 = 87oC = 360 K
P = 2 x 105 N/m2
W = PΔV
Mencari V2 :
V2/T2 = V1/T1
V2 = ( V1/T1 ) x T2 = ( 1,5/300 ) x 360 = 1,8 m3
W = PΔV = 2 x 105(1,8 − 1,5) = 0,6 x 105 = 60 x 103 = 60 kJ
Soal No. 3
2000/693 mol gas helium pada suhu tetap 27oC mengalami perubahan volume dari 2,5 liter menjadi 5 liter. Jika R = 8,314 J/mol K dan ln 2 = 0,693 tentukan usaha yang dilakukan gas helium!
Pembahasan
Data :
n = 2000/693 mol
V2 = 5 L
V1 = 2,5 L
T = 27oC = 300 K
Usaha yang dilakukan gas :
W = nRT ln (V2 / V1)
W = (2000/693 mol) ( 8,314 J/mol K)(300 K) ln ( 5 L / 2,5 L )
W = (2000/693) (8,314) (300) (0,693) = 4988,4 joule
Soal No. 4
Mesin Carnot bekerja pada suhu tinggi 600 K, untuk menghasilkan kerja mekanik. Jika mesin menyerap kalor 600 J dengan suhu rendah 400 K, maka usaha yang dihasilkan adalah....
A. 120 J
B. 124 J
C. 135 J
D. 148 J
E. 200 J
(Sumber Soal : UN Fisika 2009 P04 No. 18)
Pembahasan
η = ( 1 − Tr / Tt ) x 100 %
Hilangkan saja 100% untuk memudahkan perhitungan :
η = ( 1 − 400/600) = 1/3
η = ( W / Q1 )
1/3 = W/600
W = 200 J
Soal No. 5
Diagram P−V dari gas helium yang mengalami proses termodinamika ditunjukkan seperti gambar berikut!

Usaha yang dilakukan gas helium pada proses ABC sebesar....
A. 660 kJ
B. 400 kJ
C. 280 kJ
D. 120 kJ
E. 60 kJ
(Sumber Soal : UN Fisika 2010 P04 No. 17)
Pembahasan
WAC = WAB + WBC
WAC = 0 + (2 x 105)(3,5 − 1,5) = 4 x 105 = 400 kJ
Soal No. 6
Suatu mesin Carnot, jika reservoir panasnya bersuhu 400 K akan mempunyai efisiensi 40%. Jika reservoir panasnya bersuhu 640 K, efisiensinya.....%
A. 50,0
B. 52,5
C. 57,0
D. 62,5
E. 64,0
(Sumber Soal : SPMB 2004)
Pembahasan
Data pertama:
η = 40% = 4 / 10
Tt = 400 K
Cari terlebih dahulu suhu rendahnya (Tr) hilangkan 100 % untuk mempermudah perhitungan:
η = 1 − (Tr/Tt)
4 / 10 = 1 − (Tr/400)
(Tr/400) = 6 / 10
Tr = 240 K
Data kedua :
Tt = 640 K
Tr = 240 K (dari hasil perhitungan pertama)
η = ( 1 − Tr/Tt) x 100%
η = ( 1 − 240/640) x 100%
η = ( 5 / 8 ) x 100% = 62,5%
Soal No. 7
Sebuah mesin Carnot yang menggunakan reservoir suhu tinggi bersuhu 800 K mempunyai efisiensi sebesar 40%. Agar efisiensinya naik menjadi 50%, maka suhu reservoir suhu tinggi dinaikkan menjadi....(UMPTN 90)
A. 900 K
B. 960 K
C. 1000 K
D. 1180 K
E. 1600 K
Pembahasan
Rumus efisiensi (tanpa %)

Data dari Efisiensi pertama,
Tt = 800 K
η = 40% = 0,4 → (1 − η) = 0,6
Dari sini diperoleh suhu rendah Tr

Dari data efisiensi kedua,
η = 50% = 0,5 → (1 − η) = 0,5
Tr = 480 K
Suhu tingginya:

Soal No. 8
Sebuah mesin Carnot bekerja pada pada suhu tinggi 627°C memiliki efisiensi 50%. Agar efisiensi maksimumnya naik menjadi 70% pada suhu rendah yang tetap, maka suhu tingginya harus dinaikkan menjadi....
A. 1500°C
B. 1227°C
C. 1127°C
D. 1073°C
E. 927°C
Soal No. 9
Perhatikan gambar berikut ini!

Jika kalor yang diserap reservoir suhu tinggi adalah 1200 joule, tentukan :
a) Efisiensi mesin Carnot
b) Usaha mesin Carnot
c) Perbandingan kalor yang dibuang di suhu rendah dengan usaha yang dilakukan mesin Carnot
d) Jenis proses ab, bc, cd dan da
Pembahasan
a) Efisiensi mesin Carnot
Data :
Tt = 227oC = 500 K
Tr = 27oC = 300 K
η = ( 1 − Tr/Tt) x 100%
η = ( 1 − 300/500) x 100% = 40%
b) Usaha mesin Carnot
η = W/Q1
4/10 = W/1200
W = 480 joule
c) Perbandingan kalor yang dibuang di suhu rendah dengan usaha yang dilakukan mesin Carnot
Q2 = Q1 − W = 1200 − 480 = 720 joule
Q2 : W = 720 : 480 = 9 : 6 = 3 : 2
d) Jenis proses ab, bc, cd dan da
ab → pemuaian isotermis (volume gas bertambah, suhu gas tetap)
bc → pemuaian adiabatis (volume gas bertambah, suhu gas turun)
cd → pemampatan isotermal (volume gas berkurang, suhu gas tetap)
da → pemampatan adiabatis (volume gas berkurang, suhu gas naik)
Soal No. 10
Sejumlah gas ideal mengalami proses seperti gambar berikut.

Proses yang menggambarkan adiabatis dan isokhorik berturut-turut ditunjukkan pada nomor...(UN Fisika 2013)
A. 1 – 2 dan 3 – 4
B. 1 – 2 dan 4 – 5
C. 2 – 3 dan 1 – 2
D. 2 – 3 dan 1 – 2
E. 2 – 3 dan 3 – 4
Pembahasan
Adiabatis : proses dimana tidak ada kalor masuk atau keluar. Ciri garisnya melengkung curam. Seperti garis 2 - 3.
Isokhorik : proses pada volume tetap. Garisnya yang tegak lurus sumbu V. Bisa 5 - 1, juga 3 - 4.
Pilihan yang ada sesuai adiabatis dan isokhoris adalah 2 - 3 dan 3 - 4.
Soal No. 11

Suatu gas ideal mengalami proses siklus seperti pada gambar P − V di atas. Kerja yang dihasilkan pada proses siklus ini adalah....kilojoule.
A. 200
B. 400
C. 600
D. 800
E. 1000
Pembahasan
W = Usaha (kerja) = Luas kurva siklus = Luas bidang abcda
W = ab x bc
W = 2 x (2 x 105) = 400 kilojoule
Soal No. 12
Suatu pesawat pendingin Carnot mempunyai koefisien kinerja 6,5. Jika reservoir yang tinggi 27°C, maka reservoir yang bersuhu rendah adalah....
A. −5 °C
B. −8 °C
C. −10 °C
D. −12 °C
E. −13 °C
(Dari soal Soal UMPTN 1994)
Pembahasan
Data dari soal adalah:
Tt = 27°C = 27 + 273 = 300 K
Cp = 6,5
Tr = .....
Dari rumus koefisien performansi mesin atau pesawat pendingin:

Dimana
Cp = koefisien performansi
Tt = suhu tinggi (Kelvin)
Tr = suhu rendah (Kelvin)
Masuk datanya:

Soal No. 13
Sebuah mesin pendingin memiliki reservoir suhu rendah sebesar −15°C. Jika selisih suhu antara reservoir suhu tinggi dan suhu rendahnya sebesar 40°C, tentukan koefisien performansi mesin tersebut!
Pembahasan
Data mesin
Tr = − 15°C = (− 15 + 273) K = 258 K
Tt − Tr = 40°C
Cp =....

Soal No. 14
Sebuah kulkas memiliki suhu rendah − 13°C dan suhu tinggi 27°C. Jika kalor yang dipindahkan dari reservoir suhu rendah adalah 1300 joule, tentukan usaha yang diperlukan kulkas!
Pembahasan
Data mesin pendingin
Tr = − 13°C = (− 13 + 273) K = 260 K
Tt = 27°C = 300 K
Qr = 1300 j
W = ....
Rumus koefisien performansi jika diketahui usaha dan kalor

Dimana
W = usaha yang diperlukan untuk memindahkan kalor dari suhu rendah
Qr = kalor yang dipindahkan dari suhu rendah
Sehingga jika digabung dengan rumus dari no sebelumnya diperoleh:

sumber : http://fisikastudycenter.com/fisika-xi-sma/33-termodinamika
TERMODINAMIKA
Termodinamika adalah kajian tentang kalor (panas) yang berpindah.
Dalam termodinamika kamu akan banyak membahas tentang sistem dan
lingkungan. Kumpulan benda-benda yang sedang ditinjau disebut sistem,
sedangkan semua yang berada di sekeliling (di luar) sistem disebut
lingkungan.
Usaha Luar
Usaha luar dilakukan oleh sistem, jika kalor ditambahkan
(dipanaskan) atau kalor dikurangi (didinginkan) terhadap sistem. Jika
kalor diterapkan kepada gas yang menyebabkan perubahan volume gas,
usaha luar akan dilakukan oleh gas tersebut. Usaha yang dilakukan oleh
gas ketika volume berubah dari volume awal V1 menjadi volume akhir V2 pada tekanan p konstan dinyatakan sebagai hasil kali tekanan dengan perubahan volumenya.
W = p∆V= p(V2 – V1)
Secara umum, usaha dapat dinyatakan sebagai integral tekanan terhadap perubahan volume yang ditulis sebagai
Tekanan dan volume dapat diplot dalam grafik p – V. jika perubahan tekanan dan volume gas dinyatakan dalam bentuk grafik p – V, usaha yang dilakukan gas merupakan luas daerah di bawah grafik p – V. hal ini sesuai dengan operasi integral yang ekuivalen dengan luas daerah di bawah grafik.

Gas dikatakan melakukan usaha apabila volume gas bertambah besar (atau mengembang) dan V2 > V1. sebaliknya, gas dikatakan menerima usaha (atau usaha dilakukan terhadap gas) apabila volume gas mengecil atau V2 < V1 dan usaha gas bernilai negatif.
Energi Dalam
Suatu gas yang berada dalam suhu tertentu dikatakan memiliki energi
dalam. Energi dalam gas berkaitan dengan suhu gas tersebut dan
merupakan sifat mikroskopik gas tersebut. Meskipun gas tidak melakukan
atau menerima usaha, gas tersebut dapat memiliki energi yang tidak
tampak tetapi terkandung dalam gas tersebut yang hanya dapat ditinjau
secara mikroskopik.
Berdasarkan teori kinetik gas, gas terdiri atas partikel-partikel
yang berada dalam keadaan gerak yang acak. Gerakan partikel ini
disebabkan energi kinetik rata-rata dari seluruh partikel yang
bergerak. Energi kinetik ini berkaitan dengan suhu mutlak gas. Jadi,
energi dalam dapat ditinjau sebagai jumlah keseluruhan energi kinetik
dan potensial yang terkandung dan dimiliki oleh partikel-partikel di
dalam gas tersebut dalam skala mikroskopik. Dan, energi dalam gas
sebanding dengan suhu mutlak gas. Oleh karena itu, perubahan suhu gas
akan menyebabkan perubahan energi dalam gas. Secara matematis,
perubahan energi dalam gas dinyatakan sebagai
untuk gas monoatomik
untuk gas diatomik
Dimana ∆U adalah perubahan energi dalam gas, n adalah jumlah mol gas, R adalah konstanta umum gas (R = 8,31 J mol−1 K−1, dan ∆T adalah perubahan suhu gas (dalam kelvin).
Hukum I Termodinamika
Jika kalor diberikan kepada sistem, volume dan suhu sistem akan
bertambah (sistem akan terlihat mengembang dan bertambah panas).
Sebaliknya, jika kalor diambil dari sistem, volume dan suhu sistem akan
berkurang (sistem tampak mengerut dan terasa lebih dingin). Prinsip
ini merupakan hukum alam yang penting dan salah satu bentuk dari hukum
kekekalan energi.
Sistem yang mengalami perubahan volume akan melakukan usaha dan
sistem yang mengalami perubahan suhu akan mengalami perubahan energi
dalam. Jadi, kalor yang diberikan kepada sistem akan menyebabkan sistem
melakukan usaha dan mengalami perubahan energi dalam. Prinsip ini
dikenal sebagai hukum kekekalan energi dalam termodinamika atau disebut
hukum I termodinamika. Secara matematis, hukum I termodinamika
dituliskan sebagai
Q = W + ∆U
Dimana Q adalah kalor, W adalah usaha, dan ∆U adalah perubahan energi dalam. Secara sederhana, hukum I termodinamika dapat dinyatakan sebagai berikut.
Jika suatu benda (misalnya krupuk) dipanaskan (atau digoreng)
yang berarti diberi kalor Q, benda (krupuk) akan mengembang atau
bertambah volumenya yang berarti melakukan usaha W dan benda (krupuk)
akan bertambah panas (coba aja dipegang, pasti panas deh!) yang berarti mengalami perubahan energi dalam ∆U.
Proses Isotermik
Suatu sistem dapat mengalami proses termodinamika dimana terjadi
perubahan-perubahan di dalam sistem tersebut. Jika proses yang terjadi
berlangsung dalam suhu konstan, proses ini dinamakan proses isotermik.
Karena berlangsung dalam suhu konstan, tidak terjadi perubahan energi
dalam (∆U = 0) dan berdasarkan hukum I termodinamika kalor yang diberikan sama dengan usaha yang dilakukan sistem (Q = W).
Proses isotermik dapat digambarkan dalam grafik p – V di bawah ini. Usaha yang dilakukan sistem dan kalor dapat dinyatakan sebagai
Dimana V2 dan V1 adalah volume akhir dan awal gas.

Proses Isokhorik
Jika gas melakukan proses termodinamika dalam volume yang konstan,
gas dikatakan melakukan proses isokhorik. Karena gas berada dalam
volume konstan (∆V = 0), gas tidak melakukan usaha (W
= 0) dan kalor yang diberikan sama dengan perubahan energi dalamnya.
Kalor di sini dapat dinyatakan sebagai kalor gas pada volume konstan QV.
QV = ∆U
Proses Isobarik
Jika gas melakukan proses termodinamika dengan menjaga tekanan tetap
konstan, gas dikatakan melakukan proses isobarik. Karena gas berada
dalam tekanan konstan, gas melakukan usaha (W = p∆V). Kalor di sini dapat dinyatakan sebagai kalor gas pada tekanan konstan Qp. Berdasarkan hukum I termodinamika, pada proses isobarik berlaku
Sebelumnya telah dituliskan bahwa perubahan energi dalam sama dengan kalor yang diserap gas pada volume konstan
QV =∆U
Dari sini usaha gas dapat dinyatakan sebagai
W = Qp − QV
Jadi, usaha yang dilakukan oleh gas (W) dapat dinyatakan sebagai selisih energi (kalor) yang diserap gas pada tekanan konstan (Qp) dengan energi (kalor) yang diserap gas pada volume konstan (QV).

Proses Adiabatik
Dalam proses adiabatik tidak ada kalor yang masuk (diserap) ataupun keluar (dilepaskan) oleh sistem (Q = 0). Dengan demikian, usaha yang dilakukan gas sama dengan perubahan energi dalamnya (W = ∆U).
Jika suatu sistem berisi gas yang mula-mula mempunyai tekanan dan volume masing-masing p1 dan V1 mengalami proses adiabatik sehingga tekanan dan volume gas berubah menjadi p2 dan V2, usaha yang dilakukan gas dapat dinyatakan sebagai
Dimana γ adalah konstanta yang diperoleh perbandingan kapasitas
kalor molar gas pada tekanan dan volume konstan dan mempunyai nilai
yang lebih besar dari 1 (γ > 1).

Proses adiabatik dapat digambarkan dalam grafik p – V dengan bentuk kurva yang mirip dengan grafik p – V pada proses isotermik namun dengan kelengkungan yang lebih curam.
sumber : http://www.forumsains.com/artikel/termodinamika/
Langganan:
Postingan (Atom)